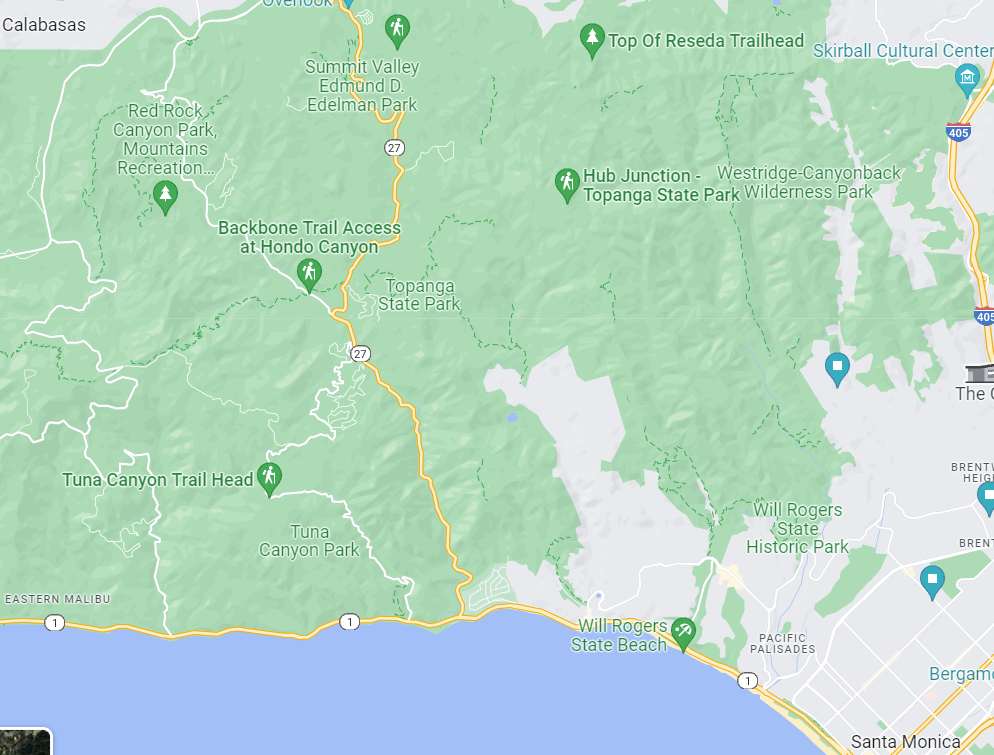
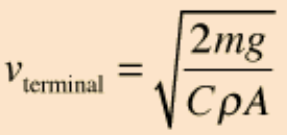In order to avoid landing on roadways, power lines, and other features of civilization, I will launch from a 14,000-acre state park.  Topanga State Park in southern California is located at 20828 Entrada Rd, Topanga, CA 90290.  The approximate GPS coordinates are 34.093160, -118.586822 .

Here is a live-updated wind map of the area.  Using the wind directions and I have chosen the state park to avoid landing the balloon in the ocean.  The state park is north of the beach, as shown in the Google map underneath the wind map.

 

The launch site will be roughly at the location of the words “Topanga State Park,” off the white roads in the Google Map image above.  

Since this is a state park, it is possible that the landing will occur in the canopy of a tall tree.  I am not yet sure how I would retrieve the payload in this case.  However, since this is a coastal chaparral biome, it is likelier that the landing will occur onto some low brush. 

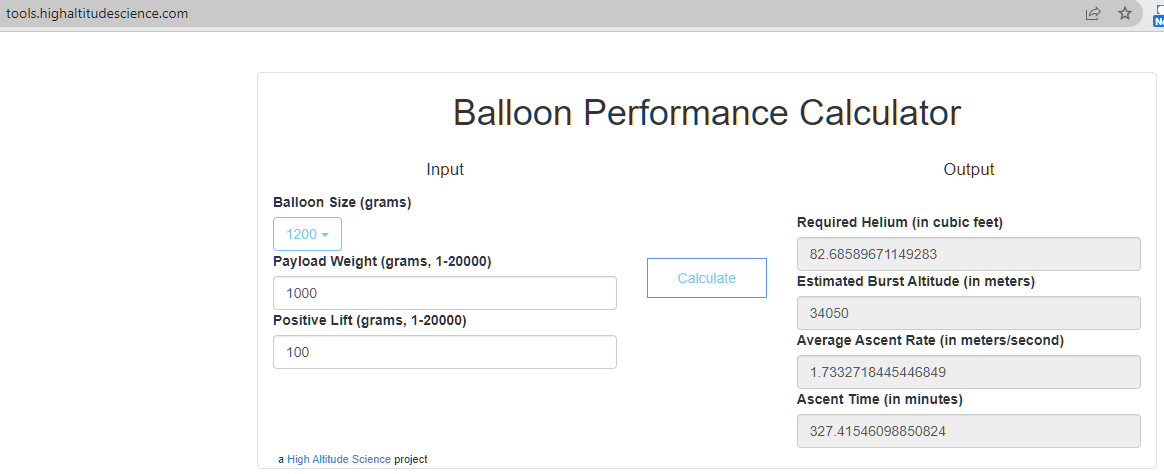
As the balloon mass is about 1200 g, and the payload mass is about 1000 g, I expect to achieve an altitude of 34 km, according to the balloon vendor‘s online calculator (screenshot below):

The burst altitude is a function of maximum balloon volume, since the balloon will expand as the external pressure decreases.  The calculated burst altitude is meant to be conservative.  According to the National Weather Service, the stratosphere begins between 5 km and 20 km above the surface of the planet, so I expect to cross into the stratosphere on this flight.

The ascent will take about five hours.  I will have to test the GoPro cameras for that longevity.  

The descent will take about nine hours.  I estimate this by using the atmospheric data from the Engineering Toolbox website, and the terminal velocity equation from an online textbook, with C=1.75 as the drag coefficient for a typical parachute.  The parachute underneath the balloon is 1.0 m in diameter, so the area of that chute is A = 3.14 square meters.  This is the only important area for the descent time estimate, since the payload presents minimal area to the wind, in comparison.

Since the Engineering Toolbox data is presented in discrete chunks of large altitude steps, I have simply added all the descent times through each chunk.  The terminal velocity is different for each chunk because of the varying air density.  Here is a link to my spreadsheet, which is also pictured below:  https://docs.google.com/spreadsheets/d/1hx36tBCp6uG9Rprfi6Rm_Ky6ANPQwNaV4uNxto6SYO8/edit?usp=sharing 

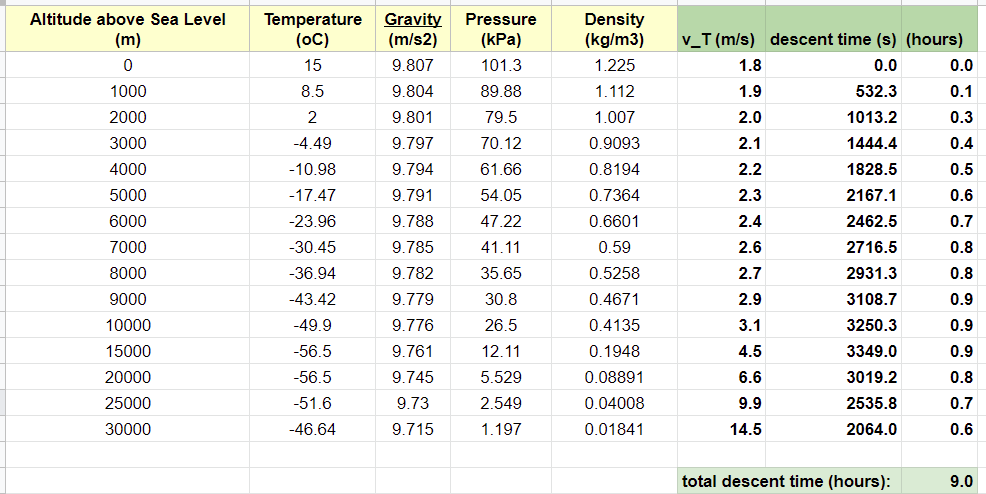
My final estimate for total flight time is 14 hours, meaning I should launch at an early morning hour and expect to retrieve the balloon the same evening.  Even with the satellite tracker on board, I might have a problem searching for the payload in the low light of the evening in the unlit state park.  I will give this problem some further thought.